Mexican wave: Crowd behaves as excitable medium
This webpage provides supplements to our results in:
Illés Farkas, Dirk Helbing, and Tamás Vicsek:
Social behaviour: Mexican waves in an excitable medium.
Nature 419, 131-132 (2002).
The information can be found also external pageherecall_made.
Abstract
The Mexican wave, or La Ola, which rose to fame during the 1986 World Cup in Mexico, surges through the rows of spectators in a stadium as those in one section leap to their feet with their arms up, and then sit down again as the next section rises to repeat the motion. To interpret and quantify this collective human behaviour, we have used a variant of models that were originally developed to describe excitable media such as cardiac tissue. Modelling the reaction of the crowd to attempts to trigger the wave reveals how this phenomenon is stimulated, and may prove useful in controlling events that involve groups of excited people.
external pageRead more on the website of Naturecall_made
external pageFull text PDFcall_made
external pageNature News articlecall_made
in Hungarian external pageTeljes cikk PDFcall_made (Fizikai Szemle)
Videos and Simulations
Mexican waves external pageon YouTubecall_made.









Background
People: an excitable medium performing the Mexican wave
The term "Mexican wave" was first used during the 1986 World Cup held in Mexico, and since then it has become a paradigm for a variety of phenomena in which an initial perturbation propagates in the form of a single "planar" wave.
The increasing popularity of this phrase, also known as La Ola, is due to its unique origin. It means a human wave moving along the stands of stadiums as one section of spectators stands up, arms lifting, then sits down as the next section does the same. The corresponding wave at a given instance involves a coordinated behaviour of hundreds, and all together tens of thousands of people as the wave makes its turn around the stadium.
For a scientist, the interesting specific feature of this spectacular phenomenon is that it represents perhaps the simplest spontaneous and reproducible behaviour of a huge crowd with a surprisingly high degree of coherence and level of cooperation. In addition, La Ola raises the exciting question of the ways by which a crowd can be stimulated to execute a particular pattern of behaviour.
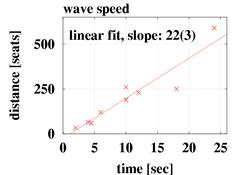
We estimated the speed of the wave from 9 videos (by T. Seidel). The slope of the fitted line below provides the speed of the wave: ( 22 ± 3 ) seats / second.
Simulation models
1. The simulation models
To describe the simulation models, we show here a small section of the tribune during an actual simulation (10 rows out of 80 and 16 "columns" of seats out of 800). The wave was triggered left from this section. By the time it has reached the section shown, the wave has already grown to the width of the entire tribune. The simulation shown here uses version A of the Detailed n-state model (see above "simulation: Mexican Wave").
The mexican wave can be decomposed into two phenomena: (i) the formation of the wave and (ii) the propagation of the wave.
The wave is usually formed by the simultaneous standing up of a small number of spectators. The spectators standing up in this group represent a small perturbation (excitation), which — depending on their neighbors — may quickly spread out. This spreading will occur only, if the audience is in the "appropriate mood" for a wave: not too bored, but not too excited either. In other words: the audience should be sitting, but "excitable". If the perturbation is amplified, then — according to our observations (14 videos of mexican waves) — during the following short time interval (less than a second) the wave will die out on one side, and survive on the other. The parameters describing the reactions of spectators to nearby excitations, e.g., neighbors jumping to their feet, are explained below.
The spontaneous symmetry breaking observed during the formation of the wave is probably due not only to the asymmetrical nature of human perception, but also to the expectations of spectators with previous experience on mexican waves and other forms of collective human behaviour. According to video recordings we have analysed, approximately 3 out of 4 mexican waves move in the clockwise direction, while 1 out 4 waves moves in the anti-clockwise direction. Being aware that numerous psychological and physical phenomena influence this symmetry breaking, we decided that for our simulations we will use the simplest model that can reproduce the (i) formation of the wave by triggering and spontaneous symmetry breaking and (ii) the stable propagation of the wave.
We have used three mexican wave models:
- Detailed n-state model / version A
- Detailed n-state model / version B
- Minimal 3-state model
2. Identical features of the models
2.1 General description
At time t person i can be in one of the following states: inactive, active, refracter. In the inactive (ground) state a person is sitting, and can be activated. An active person is moving upwards (standing up) and is not influenced by others. In the refractory state a person is sitting down or already sitting while passively recovering from the previous activity. In summary, people can influenced (activated) only in the inactive state, and they influence other people only if they are in the active state:

During a simulation update first the weighted concentration of active people within a fixed radius around each person is compared to the particular person's activation threshold. Next, if a person is inactive, then he/she can be activated using the result of this comparison and the respective model's activation rule. Each person needs a reaction time τ to update the weighted concentration of active people around him/herself.
Weights are proportional to the cosine of the direction angle of the vector pointing from the influenced inactive person to the influencing active person. People exactly to the left from a person have an influence w0 times as strong as those exactly to the right ( w0 < 1 ). Weights decay exponentially with distance: the decay length is R, and there is a cutoff at 3R. The sum of weights is 1 for each person.
2.2 Detailed description
We are using a rectangular simulation area with 80 rows and 800 "columns" of seats (units, or people). The simulation is visualized by arranging the spectators evenly on the stadium-shaped tribune. Each person is facing the inside of the stadium. The coordinate system is always local, and it is fixed to a person such that the vector (1, 0) points towards the left of the person (i.e., parallel to the rows of the stadium in the clockwise direction, if viewed from above), and the vector (0, 1) points towards the back of the person (radially out from the stadium, if viewed from above).

3. Differences between the models
3.1 The detailed n-state model
This model divides the active state into na substates and the refractory state into nr substates. Once activated, a person will deterministically step through the $n_a$ active states, then through the nr refractory states, and last it will return to the inactive state.
Activation in version A of the detailed n-state model
If the weighted concentration of neighboring active people is above a person's threshold, then the person is activated. Individual activation thresholds are used for each person. The threshold values are randomly and uniformly selected from the interval (c − Δc, c + Δc).
Activation in version B of the detailed n-state model
The activation threshold of person i is c (a constant between 0 and 1). If the weighted concentration of neighboring active people (Wi) is below c, then the person can be activated spontaenously with probability pSpont. If Wi > c, then the activation of the person will be induced with probability pInd.
3.2 The minimal 3-state model
If the weighted concentration of neighboring active people around a person is below c, then the person is activated spontaneously with probability p0−1. If Wi > c, then it is activated deterministically (with probability 1). The transition from the active to the refractory state (i.e., from state 1 to state 2) takes place with probability p1−2 at each simulation update, and the transition from the refractory to the inactive state with probability p2-0.
Contact us
Please click on our names to visit our homepages.
- external pageIllés Farkascall_made
Senior research associate at the Hungarian Academy of Sciences and Eötvös University, Budapest
- Dirk Helbing
Professor at ETH Zürich
- external pageTamás Vicsekcall_made
Professor at Eötvös University, Budapest
Group leader at the Hungarian Academy of Sciences
