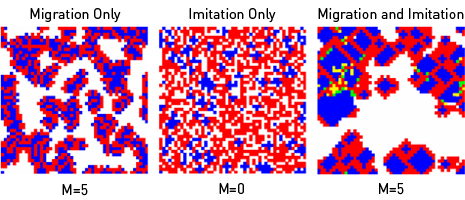
Migratory Games
The videos below are for 49x49 grids with periodic boundary conditions and a random update, assuming 40% empty sites, i.e. a density of 0.6. 49x49 grids were chosen for better visibility, while the evaluations in Fig. 2 of the manuscript were done for a 99x99 grid for comparability with Nowak's and May's spatial games [Nature 259, 826 (1992)]. The color code was also chosen as in their paper, i.e. red = defector, blue = cooperator, green = defector who became a cooperator, yellow = cooperator who turned into a defector in the last iteration. White corresponds to an empty site.
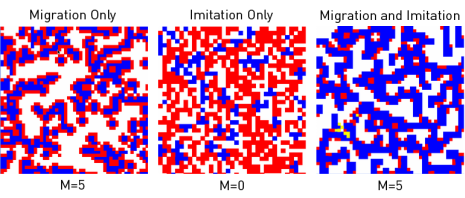
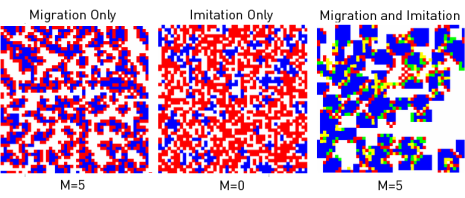
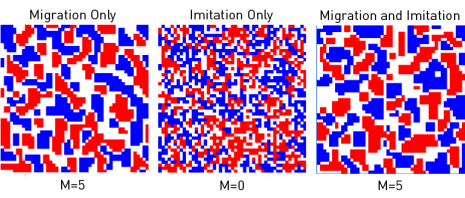
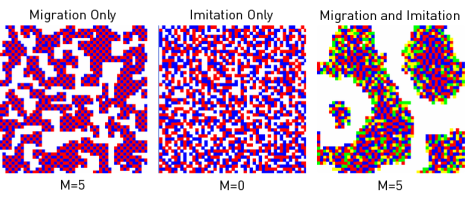
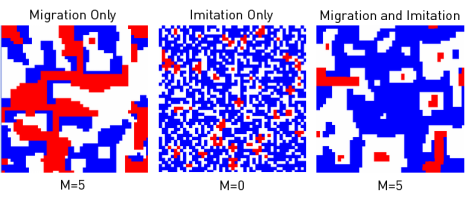
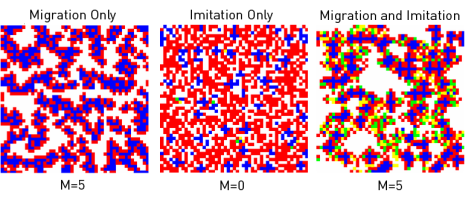
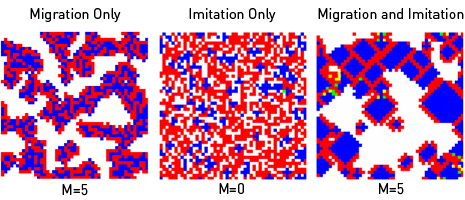
The following snapshots complement Figs. 1 and 2, and compare the migration-only case for M = 5 (left) with the imitation only case for M = 0 (center) and the combined imitation-and-migration case for M = 5 (right).
Clicking on the pictures activates the link external pageto videoscall_made animating the representative spatio-temporal dynamics.
Note that the imitation-only case shows a different dynamics in case of a parallel update.
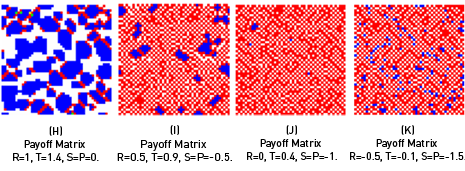
(A) Classical prisoner's dilemma
with P11 = R = 1, P12 = S = -0.2, P21 = T = 1.4, P22 = P = 0.
(B) Prisoner's dilemma according to Nowak and May with
P11 = R = 1, P12 = S = 0, P21 = T = 1.4, P22 = P = 0.

(C) P11 = R = 1, P12 = S = 0, P21 = T = 1.4, P22 = P = 0, as in B,
but the update rule is reversed, i.e. an individual first imitates, then migrates.
(D) P11 = P22 = 1, P12 = P21 = -1.
(E) P11 = P22 = 0, P12 = P21 = 1.
(F) P11=P22=P12=1, P21=-1.
(G) P11=0.59, P12 = 0.18, P21 = 1, P 22= 0, corresponding to a snowdrift game with "cost-to-benefit ratio" r = 0.7.
The following videos (which are activated by clicking on the respective snapshots) show the dynamics of game B with mobilti M = 2 and density = 0.6, if all payoff values are shifted by the same amount of C = 0 (no shift), C = -0.5, C = -1, and C = -1.5, respectively. This shift changes the dynamics and outcome of the game considerably, in contrast to conventional games with no spatial interactions.
The following videos are simulations results for success-driven motion based on wealth-based "neighborhood tagging".
(L) P11 = R = 1, P12 = S = 0, P21 = T = 1.4, P22 = P = 0, cf. B.
(M) P11 = R = 1, P12 = S = 0, P21 = T = 1.4, P22 = P = 0, as in L, but update rule is reversed, i.e. an individual first imitates, then migrates.
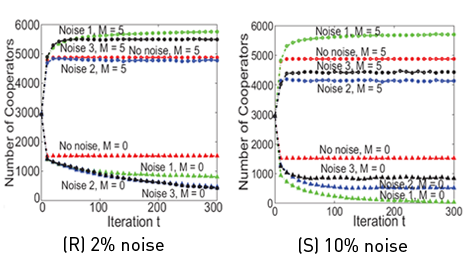
We have implemented 3 kinds of noises to test the robustness of the amplification of cooperation. In each time step, 10% of players were selected to perform the following operations after the respective migration and imitation steps.
Noise 1: The location was exchanged with a randomly chosen neighboring site.
Noise 2: Cooperation was replaced by defection and vice versa to reflect "mutation".
Noise 3: The selected players were removed from the grid and an equal number of players was created at randomly chosen free sites, in order to mimic birth and death process. The newly born palyers has a 50% chance to be cooperators and a 50% chance to be defectors.
(N) No Noise T = 1.3, R = 1, p = 0, S = 0
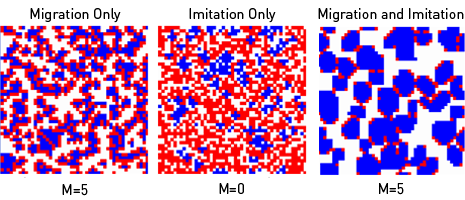
(O) Noise 1 T = 1.3, R = 1, p = 0, S = 0

(P) Noise 2 T = 1.3, R = 1, p = 0, S = 0
(Q) Noise 3 T = 1.3, R = 1, p = 0, S =0

The following figures show the effect of noise on the number of cooperators.
The following videos are simulation results fot the conventional Prisoner's Dilemma with P > S.
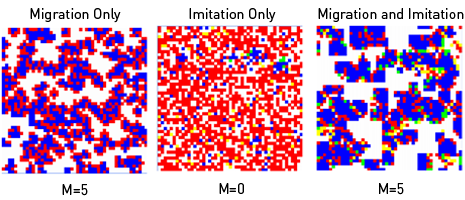
(T) No noise T = 1.3, R = 1, P = 0.1, S = 0
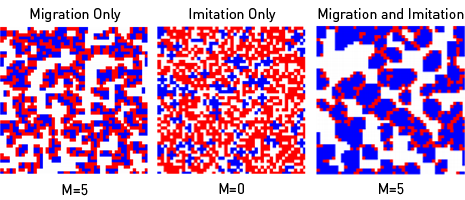
(U) Noise 1 T = 1.3, R = 1, P = 0.1, S = 0
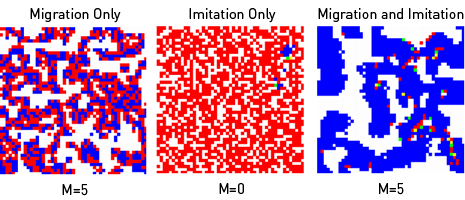
(V) Noise 2 T = 1.3, R = 1, P = 0.1, S = 0
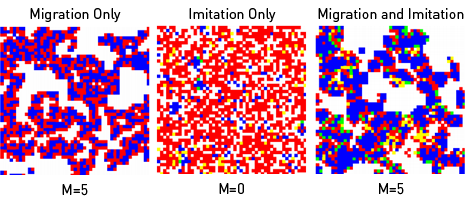
(W) Noise T = 1.3, R = 1, P = 0.1, S = 0
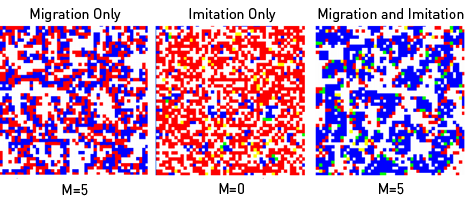
Impact of “globalization” on cooperation in the migratory prisoner’s dilemma with imitation and noise 3 (with q = 0.05).
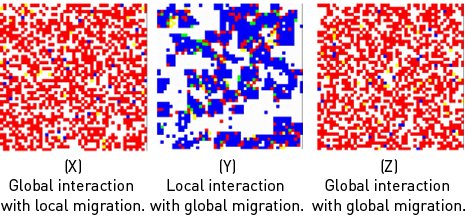
Analytical calculations for a simplified model of strategic interaction in space with success-driven migration and diffusion (read external page"Pattern formation, social forces, and diffusion instability in games with success-driven motion"call_made).
