The outbreak of cooperation among success-driven individuals under noisy conditions (Supporting Information)
This is the supplementary webpage to the publication on The Outbreak of Cooperation in external pagePNAS.
Description of cover figure: Illustration of self-organized pattern formation in migration games. The snapshot, taken after 200 time steps, shows the outcome of the spatial interaction of mobile individuals, who strategically interact with their four nearest neighbors and copy the strategy of their most successful neighbor. The simulation assumes that individuals earn no payoff, if they meet individuals who use the same strategy, while their outcome is positive, if interacting with individuals using another strategy. Strategy 1 is represented by blue disks, strategy 2 by red disks. A change to strategy 2 in the last time step is indicated in green, a change to strategy 2 by yellow. White spaces are empty. Individuals perform success-driven migration, i.e. they move to empty locations with a higher expected payoff. The maximum migration distance in one time step was assumed to be 5. Starting with uniformly distributed strategies, one observes an agglomeration of individuals, and individuals with different strategies mix. This is to be distinguished from the migratory dynamics in other spatial games, which lead to segregation patterns, for example, as studied by Nobel prize winner Thomas Schelling. For animated videos see /migrationgames.
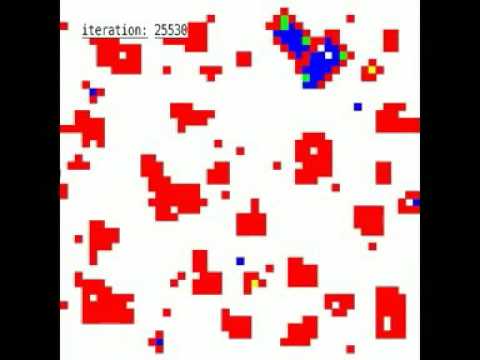
Spontaneous outbreak of prevalent cooperation in the spatial prisoner's dilemma with random relocations and strategy mutations. The prisoner's dilemma describes social interactions, in which it is risky to cooperate and tempting to defect (i.e. to cheat or free-ride). The simulations are for 49x49-grids (red = defector, blue = cooperator, white = empty site, green = defector who became a cooperator, yellow = cooperator who turned into a defector in the last iteration). The simulation starts with the initial configuration of a circular cluster of defectors (red) at time t=0. In each time step (iteration), the strategies and locations of all individuals have been updated in a random sequential order. The video shows one snapshot every time step. In Phase I, the cluster of defector splits up, and defectors disperse over the space due to random relocations. Nevertheless, small defective clusters are formed, as the payoff for mutual defection is higher than when defectors do not have any neighbors. Cooperators are generated randomly at a very small rate due to strategy mutations (green), but usually turn into defectors quickly (yellow). The video is cut, because the features of the spatio-temporal patterns do not change over more than 20,000 iterations. Phase II is displayed more slowly to highlight the sudden outbreak of cooperation: Around the time t=25,510, a small, but overcritical cluster of cooperators appears in the upper right corner (green and blue). This happens by random coincidence of strategy mutations, which creates cooperators in neighboring locations by chance. The overcritical cluster of cooperators (blue) does not only allow cooperators to survive; neighboring defectors also start to imitate them due to their greater payoff (green). The evolution in Phase III is shown again at the previous movie speed: Once a large enough cooperative cluster has appeared, cooperation is "exported" to other locations by random and success-driven migration, and it spreads quickly among individuals almost everywhere. For more videos see /migrationgames
Related Publications:
[1] D. Helbing (1992) A mathematical model for behavioral changes by pair interactions. Pages 330-348 in: G. Haag, U. Mueller, and K. G. Troitzsch (eds.) Economic Evolution and Demographic Change. Formal Models in Social Sciences (Springer, Berlin).
[2] D. Helbing (1993) external pageStochastic and Boltzmann-like models for behavioral changes, and their relation to game theory. external pagePhysica A 193, 241-258.
[3] D. Helbing (1996) external pageA stochastic behavioral model and a `microscopic' foundation of evolutionary game theory. external pageTheory and Decision 40, 149-179.
[4] D. Helbing (1998) Microscopic foundation of stochastic game dynamical equations. Pages 211-224 in: W. Leinfellner and E. Köhler (eds.) external pageGame Theory, Experience, Rationality (Kluwer Academic, Dordrecht).
[5] D. Helbing and T. Vicsek (1999) external pageOptimal self-organization. external pageNew Journal of Physics 1, 13.1-13.17.
[6] D. Helbing and T. Platkowski (2000) external pageSelf-organization in space and induced by fluctuations. external pageInternational Journal of Chaos Theory and Applications 5(4), 47-62.
[7] D. Helbing and T. Platkowski (2002) external pageDrift- or fluctuation-induced ordering and self-organisation in driven many-particle systems. external pageEurophysics Letters (EPL) 60, 227-233.
[8] D. Helbing (2009) external pagePattern formation, social forces, and diffusion instability in games with success-driven motion external pageEuropean Physical Journal B 67, 345–356.
[9] W. Yu and D. Helbing (2009) Game theoretical interactions of moving agents. Forthcoming.
[10] D. Helbing, M. Schönhof, H.-U. Stark, and J. A. Holyst (2005) external pageHow individuals learn to take turns: Emergence of alternating cooperation in a congestion game and the prisoner's dilemma. external pageAdvances in Complex Systems 8, 87-116.
[11] D. Helbing, M. Schönhof, and D. Kern (2002) external pageVolatile decision dynamics: Experiments, stochastic description, intermittency control, and traffic optimization. external pageNew Journal of Physics 4, 33.1-33.16.
[12] D. Helbing (2004) external pageDynamic decision behavior and optimal guidance through information services: Models and experiments. Pages 47-95 in: M. Schreckenberg and R. Selten (eds.) external pageHuman Behaviour and Traffic Networks (Springer, Berlin).
[13] D. Helbing (1994) external pageA mathematical model for the behavior of individuals in a social field. external pageJournal of Mathematical Sociology 19 (3), 189-219.
[14] D. Helbing (1993) external pageBoltzmann-like and Boltzmann-Fokker-Planck equations as a foundation of behavioral models. external pagePhysica A 196, 546-573.